进制转换是学习计算机的基础,了解并掌握计算机进制掌握非常有必要。
(一)数制
计算机采用的是二进制,因此二进制具有运算简单,易实现且可靠。还有八进制、十六进制作为二进制的缩写。一般计数都采用进位计数,其特点是:(逢N进一)二进制:逢二进一,借一当二。八进制:逢八进一,借一当八。十六进制:逢十六进一,借一当十六。
(二)数制转换:转换前两数相等,转换后仍必须相等。
十进制:有十个基数,0123456789。
二进制:有两个基数,01。
八进制:有八个基数,01234567。
十六进制:有十六个基数,0——9,A——F。(A=10,B=11,C=12,D=13,E=14,F=15)
一:十进制与二进制间的转换
(1)十进制→二进制:十进制数除以2,初至0时所得余数按反方向写出,即为二进制数。
(2)二进制→十进制: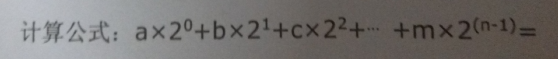
以上公式中,a表示二进制数右边第一位的数,b表示二进制数的右边第二位的数,,,,,,,m表示二进制数的右边第(n-1)位的数。
| 二进制右数数位 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| 十进制数 | 1 | 2 | 4 | 8 | 16 | 32 | 64 | 128 | 256 |
| 公式原型 | 2的0次方 | 2的1次方 | 2的2次方 | 2的3次方 | 2的4次方 | 2的5次方 | 2的6次方 | 2的7次方 | 2的8次方 |
二:十进制与八进制间的转换
(1)十进制→八进制:十进制数主次整除8,直至商为0,所得余数按照相反顺序写出,即为其八进制数。
(2)八进制→十进制:公式同二进制转十进制。
| 二进制右数第n数位 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 公式原型 8的(n-1)次方 | 8的0次方 | 8的1次方 | 8的2次方 | 2的3次方 | 8的4次方 | 8的5次方 | 8的6次方 | 8的7次方 |
| 十进制下的实际数 | 1 | 8 | 64 | 512 | 4096 | 32768 | 262144 | 2097152 |
三:十进制与十六进制间的转换
(1)十进制→十六进制:十进制数整除16,直至商为0,所得余数按相反顺序写出,即为十六进制数。例:75的十六进制数为4B。
(2)十六进制→十进制:同二进制、八进制转十进制一样。
| 十六进制右数第n数位 | 1 | 2 | 3 | 4 |
| 公式原型 16的(n-1)次方 | 1 | 16 | 256 | 4096 |
例:1BC2由右至左成为十进制为7106。
四:其他进制之间转换
(一)二进制与八进制间
(1) 二进制→八进制:对于整数,采用从右到左每三位一组,不够三位的在其左边补齐0,每组单独转换出来,即为八进制数。
例:(001 101 111 011)
1 5 7 3
(2)八进制→二进制:将每位八进制由三位二进制数代替,即可完成转换。
例:( 1 7 3 5 )
001 111 011 101
(二)二进制与十六进制间
(1)二进制→十六进制:将二进制数的没四位用一个十六进制数码来表示,整数部分以小数点为界点从右往左每四位一组转换,小数部分从小数点开始自左向右每四位一组进行转换。
例:(1001 0111 0111 1001)
9 7 7 9
(2)十六进制→二进制:只要将每一位十六进制数用四位相应的二进制数表示,即可完成转换。
例:( 8 7 6 5 )
1000 0111 0110 0101
【规律】1.十进制与二进制、八进制、十六进制间可相互转化,二进制与八进制、十进制、十六进制间可相互转化,但八进制与十六进制间不可直接转化,必须以二进制或十进制作为工具,一般采用因简便多二进制。
2.二进制与八进制转化注意是3个位数,二进制与十六进制转化注意是4个位数。